# 回溯算法解题套路框架
废话不多说,直接上回溯算法框架。 解决一个回溯问题,实际上就是一个决策树的遍历过程。 你只需要思考 3 个问题:
- 路径:也就是已经做出的选择
- 选择列表:也就是你当前可以做的选择
- 结束条件:也就是到达决策树底层,无法再做选择的条件
如果你不理解这三个词语的含义也没有关系,后面我们会用「全排列」和「N 皇后问题」这两个经典的回溯算法问题来帮你理解这些词语是什么意思,现在你先留着印象。
代码方面,回溯算法的框架:
`
result = []
function backtrack(路径,选择列表) {
if 满足结束条件:
result.push(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径,选择列表)
撤销选择
}
`
其核心就是 for 循环里面的递归,在递归调用之前「做选择」,在递归调用之后「撤销选择」 ,特别简单。
什么叫做选择和撤销选择呢,这个框架的底层原理是什么呢?下面我们就通过「全排列这个问题来解开之前的疑惑,详细探究一下其中的奥妙!
# 全排列问题
我们在高中的时候就做过排列组合的数学题,我们也知道 n 个不重复的数,全排列共有 !n 个。
ps:为了简单清晰,我们这次讨论的全排列问题不包含重复数字。
那么我们当时怎么穷举全排列呢?比方说给三个数:[1, 2, 3] ,你肯定不会无规律地乱穷举,一般是这样:
先固定第一位为 1,然后第二位可以是 2,那么第三位只能是 3;然后可以把第二位变为 3,第三位就只能是 2 了;然后在变化第一位 ...
其实这就是回溯算法,我们高中无师自通就会用,或者有的同学直接画出下面这棵回溯树:
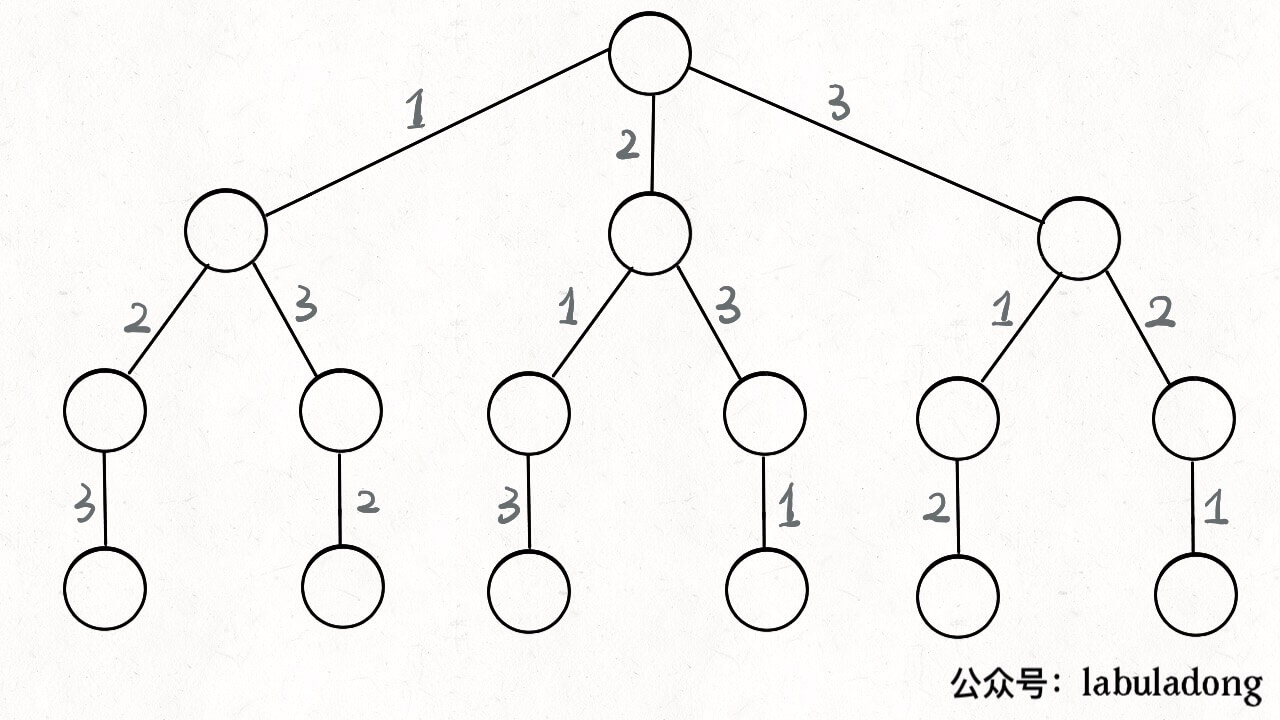
只要从根遍历这棵树,记录路径上的数字,其实就是所有的全排列。 我们不妨把这棵树称为回溯算法的「决策树」。
为什么说这是决策树呢,因为你在每个节点其实都在做决策。 比如你站在下图中的红色节点上:

你现在就在做决策,可以选择 1 那条分支也可以选择 3 那条分支,但为什么只能在 1 和 3 种选择呢,因为 2 这个树枝已经选择过了,而全排列中不允许出现重复数字。
现在可以解答开头的几个名词: [2] 就是「路径」,记录你已经做过的选择; [1, 3] 就是「选择列表」,表示你当前可以做出的选择;「结束条件」就是遍历到树的底层,在这里就是选择列表为空的时候。
如果明白了这几个名词,可以把「路径」和「选择」列表作为决策树上每个节点的属性,比如下图列出了几个节点的属性:

我们定义的 backtrack 函数其实就像一个指针,在这棵树上游走,同时要正确维护每个节点的属性,每当走到树的底层,其「路径」就是全排列中的一员。
再进一步就是如何遍历一棵树?这个应该不难吧。回忆一下之前「学习数据结构的框架思维」写过,各种搜索问题其实都是树的遍历问题,而多叉树的遍历框架就是这样:
`
function traverse(root) {
for(node in root.children) {
// 前序遍历
travese(node)
// 后序遍历
}
}
`
而所谓的前序遍历和后序遍历,他们只是两个很有用的时间点,我给你画张图你就明白了:

前序遍历的代码在进入某个节点之前的那个时间点执行,后序遍历代码在离开某个节点之后的那个时间点执行。
回想我们刚才说的,「路径」和「选择」是每个节点的属性,函数在书上游走要正确维护节点的属性,那么就要在这两个特殊时间点搞点动作:

现在,你是否理解了回溯算法的这段核心框架:
`
for 选择 in 选择列表:
# 做选择
将该选择从选择列表移除
路径.add(选择)
backtrack(路径,选择列表)
# 撤销操作
路径.remove(选择)
将该选择再加入选择列表
`
我们只要在递归之前做出选择,在递归之后撤销刚才的选择 ,就能正确得到每个节点的选择列表和路径。
下面直接看全排列代码:
function permute(nums: number[]): number[][] {
const result: number[][] = []
function backtrack(track: number[]): void {
if(track.length === nums.length) {
result.push(track)
return
}
for(const num of nums) {
if(track.includes(num)) continue
track.push(num)
backtrack(track.slice())
track.pop()
}
}
backtrack([])
return result
}
画出整棵决策树:

至此,我们通过全排列问题详解了回溯算法的底层原理。当然这个算法全排列不是很高效,因为对数组使用了 includes 方法需要 O(n) 的时间复杂度。但是必须要说明的是,不管怎么优化,都符合回溯框架,而且时间复杂度不可能低于 O(N!) ,因为穷举整棵决策树是无法避免的。 这也是回溯算法的一个特点,不想动态规划存在重叠子问题可以优化,回溯算法就是纯暴力穷举,复杂度一般都很高。
明白了全排列问题,就可以直接套回溯算法框架,下面简单看看 N 皇后问题。
# N 皇后问题
这个问题很经典了,简单解释一下:给你一个 N×N 的棋盘,让你放置 N 个皇后,使得它们不能互相攻击。
PS:皇后可以攻击同一行、同一列、左上左下右上右下四个方向的任意单位。
这个问题本时尚和全排列问题差不多,决策树的每一层表示棋盘上的每一行,每个节点可以做出的选择时在该行的任意一列放置一个皇后。
直接套用框架:
function solveNQueens(n: number): string[][] {
const res: string[][] = []
function backtrack(board: string[], row: number): void {
// 触发结束条件
if (row === n) {
res.push(board)
return
}
for (let col = 0; col < n; col++) {
// 排除不合法选择
if (!isValid(board, row, col)) continue
const letter = board[row].split('')
// 做选择
letter[col] = 'Q'
board[row] = letter.join('')
// 进入下一行选择
backtrack(board.slice(), row + 1)
// 撤销选择
letter[col] = '.'
board[row] = letter.join('')
}
}
// 是否可以在 board[row][col] 放置皇后
function isValid(board: string[], row: number, col: number): boolean {
for (let i = 0; i < n; i++) {
// 检查是否有皇后互相冲突
if (board[i][col] === 'Q') return false
}
for (let i = row - 1, j = col + 1; i >= 0 && j < n; i-- , j++) {
// 检查右上方是否有皇后互相冲突
if (board[i][j] === 'Q') return false
}
for (let i = row - 1, j = col - 1; i >= 0 && j >= 0; i-- , j--) {
// 检查左上方是否有皇后互相冲突
if (board[i][j] === 'Q') return false
}
return true
}
// 初始化每一项为 n 个 '.',并且当前为第 0 行
backtrack(Array(n).fill('.'.repeat(n)), 0)
return res
};
函数 backtrack 依然像个决策树上游走的指针,通过 row 和 col 就可以表示函数遍历到的位置,通过 isValid 函数可以将不符合条件的情况剪枝:

# 最后总结
回溯算法就是个多叉树的遍历问题,关键就是在前序遍历和后序遍历的位置坐操作。
写 backtrack 函数时,需要维护走过的「路径」和当前可以做的「选择列表」,当触发「结束条件」时,将「路径」记入结果集。
其实想想看,回溯算法和动态规划是不是有点像呢?我们在动态规划系列文章中多次强调,动态规划的三个需要明确的点就是「状态」「选择」和「base case」,是不是就对应着走过的「路径」,当前的「选择列表」和「结束条件」?
某种程度上说,动态规划的暴力求解阶段就是回溯算法。只是有的问题具有重叠子问题性质,可以用 dp table 或者备忘录优化,将递归树大幅剪枝,这就变成了动态规划。而今天的两个问题,都没有重叠子问题,也就是回溯算法问题了,复杂度非常高是不可避免的。