时间复杂度

常见的 7 种时间复杂度

• O(1) 常数复杂度
• O(log n) 对数复杂度
• O(n) 线性时间复杂度
• O(n^2) 平方
• O(n^3) 立方
• O(2^n) 指数
• O(n!) 阶乘

最简单判断时间复杂度的方法：查看当前函数执行的次数

我们不需要考虑常数系数，即

O(2n) === O(n)

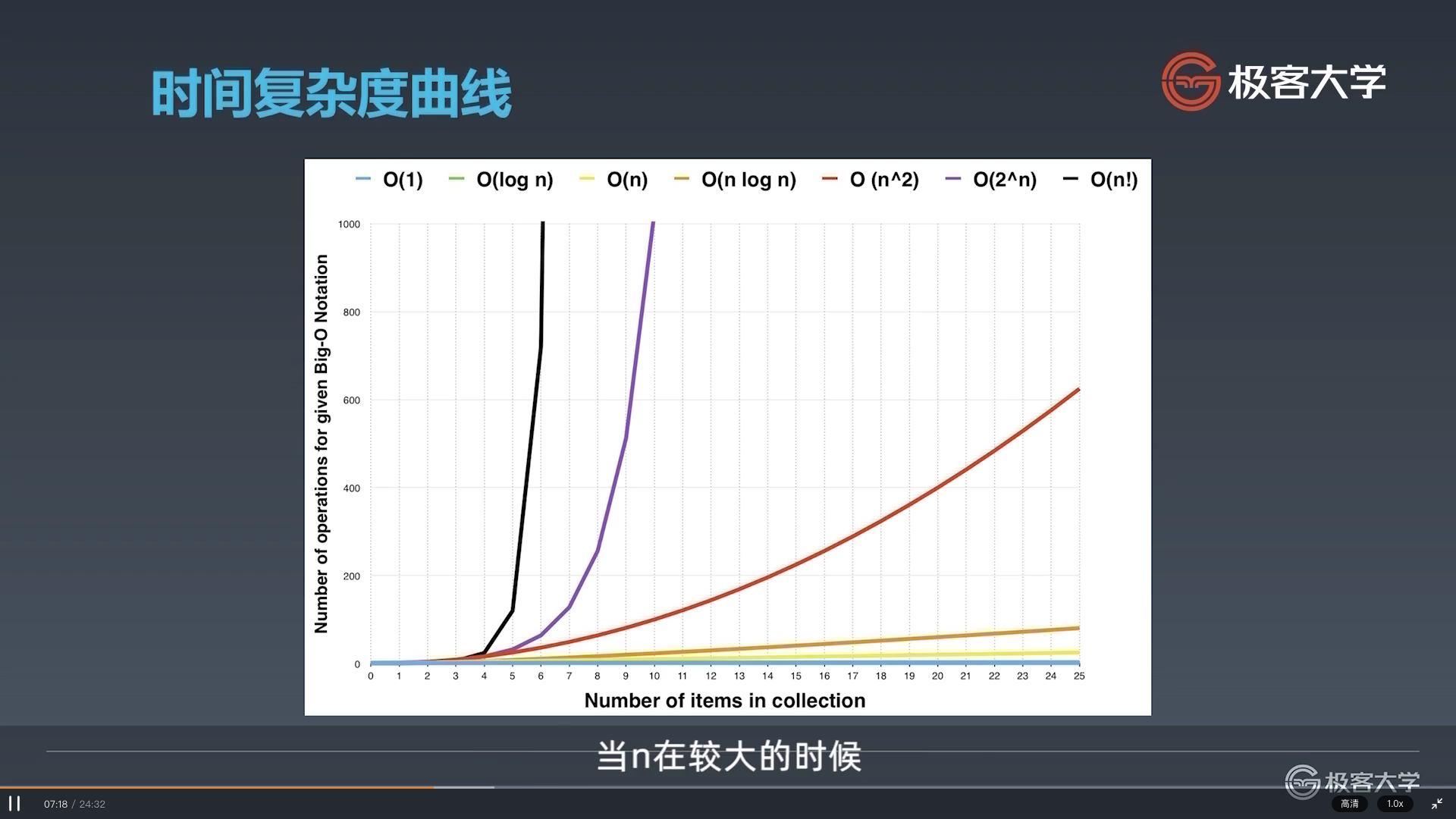
所以，我们在写程序的时候，需要严格的考虑时间空间复杂度。

计算 1 + 2 + 3 + 4 + ... + n

1. 从 1 到 n 的循环累加

   let res = 0
   for(let i = 1; i <= n; i++ ) {
     res += i
   }
   

   因为进行了 n 次循环，所以时间复杂度是 O(n)。

2. 求和公式 sum = n * (n + 1) / 2

   程序只执行了一次，所以时间复杂度是 O(1)。

面试四要素

1. 首先和面试官确认题目的意思
2. 想尽所有可能解决的方案
3. 比较各个方法之间的时间和空间复杂度，找出最优的解决方案
4. 测试结果

递归

核心：理解递归直线了多少次。

方法：利用递归的执行顺序，画出递归的树形结构，称之为递归状态树。

求斐波那契数列

递推公式：F(n) = F(n - 1) + F(n - 2)

分析最简单的解决方案：

function fib(n: number): number {
  if(n < 2) return n
  return fib(n - 1) + fib(n - 2)
}

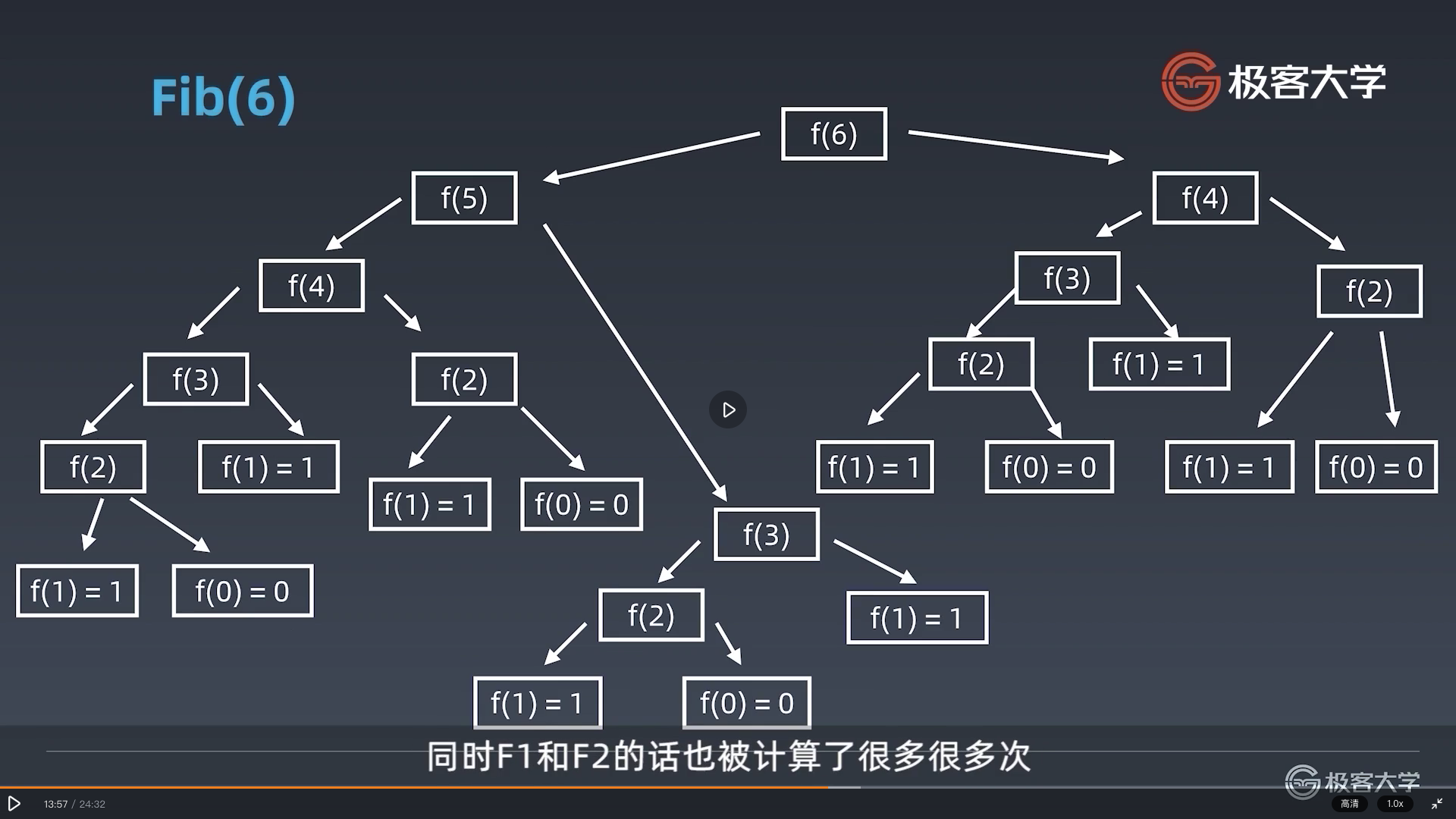
我们可以看到两个现象：

1. 每多展开一层，节点数比上一层多一倍，所以大概判断在第 n 层的节点数为 2 ^ n 次方个，呈指数型增长；
2. 各层之间的节点存在重复出现的节点 ，所以有非常多的冗余数据

主定理 (opens new window)

任何递归、分治的方法都可以使用主定理来计算时间复杂度

主要有下面四种情况：

翻译成中文：

算法	时间复杂度	递推公式	解释
二分查找	O(logn)	T(n) = T(n / 2) + O(1)	每次都一分为二，越分越小
二叉树遍历	O(n)	T(n) = 2 * T(n / 2) + O(1)	每次都一分为二，但是每一边都是相等的时间复杂度
排序二维矩阵二分查找	O(n)	T(n) = 2 * T(n / 2) + O(logn)	一维二分查找的平方
归并排序	O(nlogn)	T(n) = 2 * T(n / 2) + O(n)

面试题

• 二叉树的前序、中序、后序遍历的时间复杂度

  O(n)：二叉树的每个节点有且仅访问一次

• 图的遍历时间复杂度

  O(n)：图中的每个节点有且仅访问一次

• 搜索算法：DFS（深度优先）、BFS（广度优先） 时间复杂度是多少？

  都是 O(n)，因为每个节点都只复杂一次。

• 二分查找的时间复杂度

  O(logn)

空间复杂度

关键点：

1. 数组的长度
2. 递归的深度