# 动态规划答疑篇
这篇文章就给你讲明白读者问的最多的两个问题:
- 到底什么才叫「最优子结构」,和动态规划有什么关系
- 为什么动态规划遍历 dp 数组的方式五花八门,有正着遍历,有倒着遍历,有斜着遍历,有的无论怎么遍历都是对的。
# 最优子结构详解
「最优子结构」是某些问题的一种特定性质,并不是动态规划问题专有的。也就是说,很多问题其实都有最优子结构,只是其中大部分不具有重叠子问题,所以我们不把它们归为动态规划系列问题而已。
我们先举个很容易理解的例子:假设你们学校有 10 个班,你已经计算出了每个班的最高考试成绩。那么现在我要求你计算全校最高的成绩,你会不会算?当然会,而且你不用重新遍历全校学生的分数进行比较,而是只要在这 10 个最高成绩中取最大的就是全校的最高成绩。
我给你提出的问题就 符合最优子结构 :可以从子问题的最有结果推出更大规模问题的最优结果。让你算 每个班 的最优成绩就是子问题,你知道所有子问题的答案后,就可以借此推出 全校 学生的最优成绩这个规模更大的问题的答案。
你看,这么简单的问题都有最优子结构性质,只是因为显然没有重叠子问题,所以我们简单的求最值肯定不用动态规划。
再举个例子,假设你们学校有 10 个班,你已知每个班的最大分数差(最高分和最低分的差值),那么现在我让你计算全校学生中的最大分数差,你会不会算?可以想办法算,但是肯定不能通过已知的这 10 个班的最大分数差推算出来,因为这 10 个班的最大分数差不一定就包含全校学生的最大分数差。
这次我给你提出的问题就 不符合最优子结构 ,因为你没办法通过每个班的最优值推导出全校的最优值,没办法通过子问题的最优值推导出规模更大的问题的最优值。前文「动态规划详解」说过,想满足最优子解,子问题之间必须互相独立。全校的最大分数差可能出现在两个班之间,显然子问题并不独立,所以这个问题本身不符合最优子结构。
那么遇到这种最优子结构失效情况,怎么办?策略是:改造问题。 对于最大分数差的这个问题,我们不是没办法利用已知的每个班的分数差吗,那我只能这样写一段暴力代码:
int result = 0
for(Student a : school) {
for(Student b : school) {
if(a is b) continue
result = max(result, |a.score - b.score|)
}
}
return result
改造问题,也就是把问题等价转化:最大分数差,不就等价于最高分数和最低分数的差么,那不就是要求最高和最低分数么,不就是我们讨论的第一个问题么,不就具有最优子结构么?那么现在改变思路,借助最优子结构解决最值问题,再回过头解决最大分数差问题,是不是就高效的多了。
当然,上面的这个例子太简单了,不过请读者回顾一下,我们做动态规划问题,是不是一直在求各种最值,本质上和我举的例子没有什么区别,无非需要处理一下重叠子问题。
再举个常见但也十分简单的例子,求一棵二叉树的最大值(简单起见,假设节点的值都是非负数):
function maxVal(root: TreeNode | null): number {
if(!root) return -1
const left = maxVal(root.left)
const right = maxVal(root.right)
return Math.max(root,val, left, right)
}
你看这个问题也符合最优子结构,以 root 为根的树的最大值,可以通过两边子树(子问题)的最大值推导出来,结合刚才学校和班级的例子,应该更加容易理解。
当然这也不是动态规划问题,旨在说明,最优子结构并不是动态规划独有的一种性质,能求最值的问题大部分都具有这个性质; 但反过来,最优子结构性质作为动态规划问题的必要条件,一定是让你求最值的。 以后碰到那种恶心人的最值题,思路往动态规划想就对了,这就是套路。
动态规划不就是从最简单的 base case 往后推到吗,可以想象成一个链式反应,不断以小博大,但是只有符合最优子结构问题,才有发生这种链式反应的性质。
找到最优子结构的过程,其实就是证明状态转移方程正确性的过程,方程符合最优子结构就可以写暴力解,写出暴力解就可以看出又没有重叠子问题,有则优化,无则 OK。这也是套路,经常刷题的朋友应该能体会。
# dp 数组的遍历方向
我相信读者做动态规划题目时,肯定会对 dp 数组的遍历顺序有些头疼。我们拿二位 dp 数组距离,有时我们是正向遍历:
for(let i = 0; i < m; i++) {
for(let j = 0; j < n; j++) {}
}
有时候我们反向遍历
for(let i = m - 1; i >=0; i--) {
for(let j = n - 1; j >=0; j--) {}
}
有时候可能会斜向遍历
for(let l = 2; l <=n ; l++) {
for(let i = 0; i <= n - 1; i++) {
const j = l + i - 1
}
}
甚至更让人迷惑的是,有时候发现正向反向遍历都可以得到正确答案,比如「团灭 LeetCode 股票买卖问题」中有的地方就正反皆可。
那么,如果仔细观察的话,可以发现其中的原因,你只要把握住两点即可:
- 遍历的过程中,所需的状态必须是已经计算出来的
- 遍历的终点必须是存储结果的那个位置
下面来具体解释上面两个原则是什么意思。
比如编辑距离这个经典问题,我们通过对 dp 数组的定义,确定了 base case 是 dp[...][0] 和 dp[0][...] ,最终答案是 dp[m][n] ;而且我们通过状态转移方程知道 dp[i - 1][j] , dp[i][j - 1] ,dp[i - 1][j - 1] 转移而来,如下图:
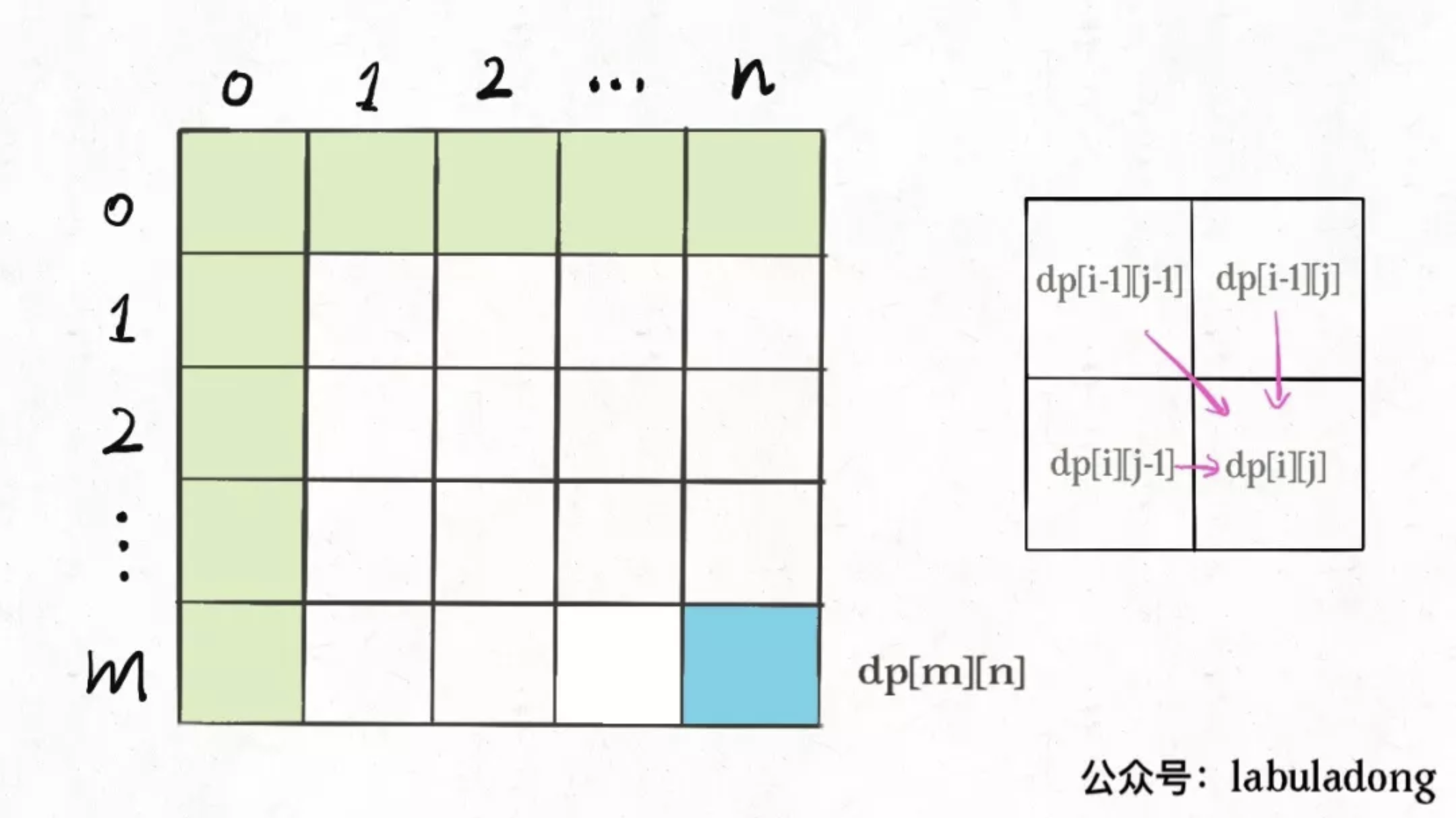
那么,参考刚才说的两条原则,你该怎么遍历 dp 数组?肯定是正向遍历:
for(let i = 1; i < m; i++) {
for(let j = 1; j < n; j++) {
}
}
因为,这样每一步迭代的左边、上边、左上边的位置都是 base case 或者之前计算过的,而且作中结束在我们想要的答案 dp[m][n] 。
再举一个例子,回文子序列问题:最长回文子序列,我们通过对 dp 数组的定义,确定了 base case 处在中间的对角线, dp[i][j] 需要从 dp[i + 1][j] 、dp[i][j - 1] 、 dp[i + 1][j - 1] 、 dp[i + 1][j - 1] 转移而来,想要求的最终答案是 dp[0][n - 1] 如下图:
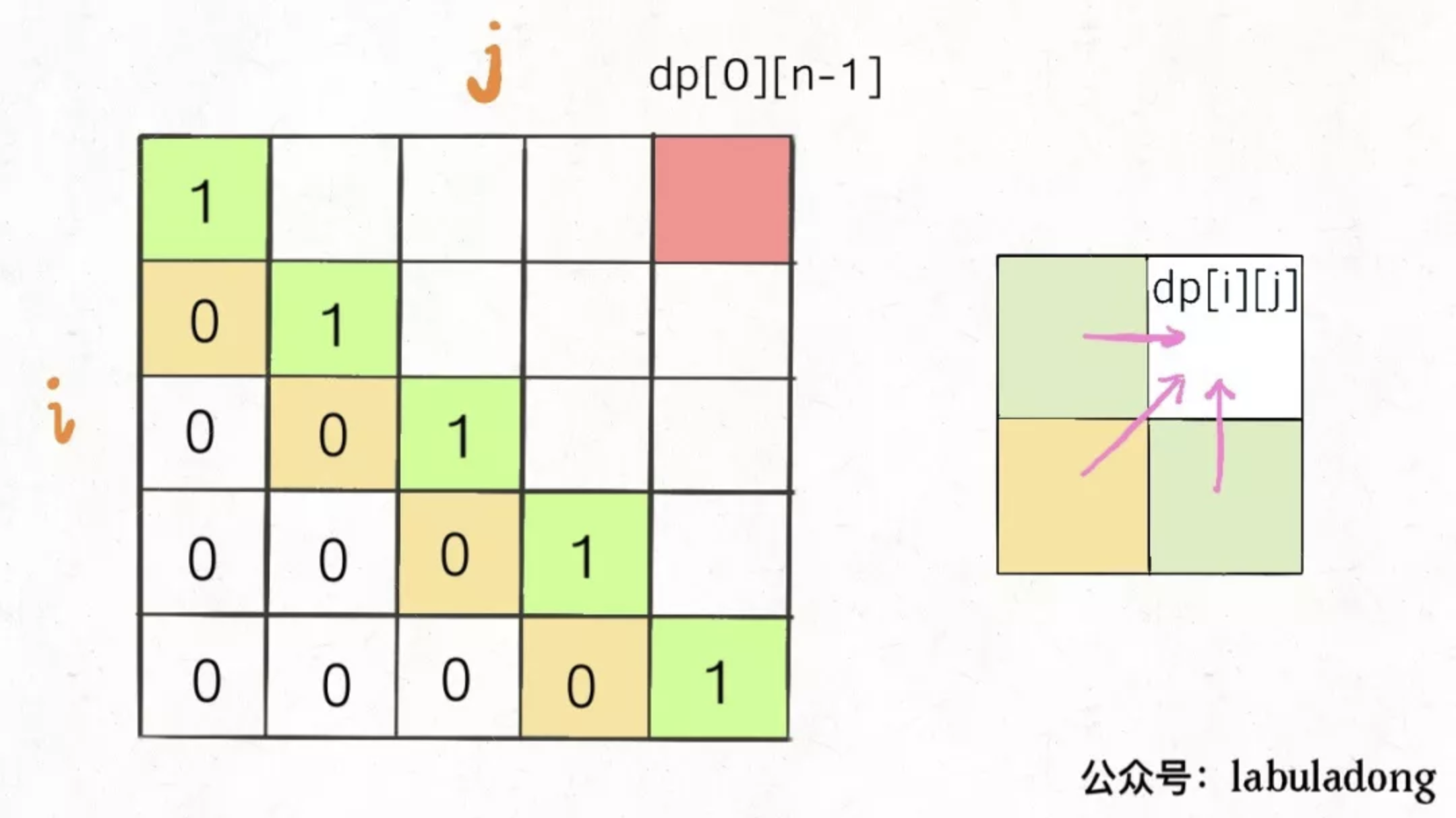
这种情况根据刚才的两个原则,就可以有两种正确的遍历方式:
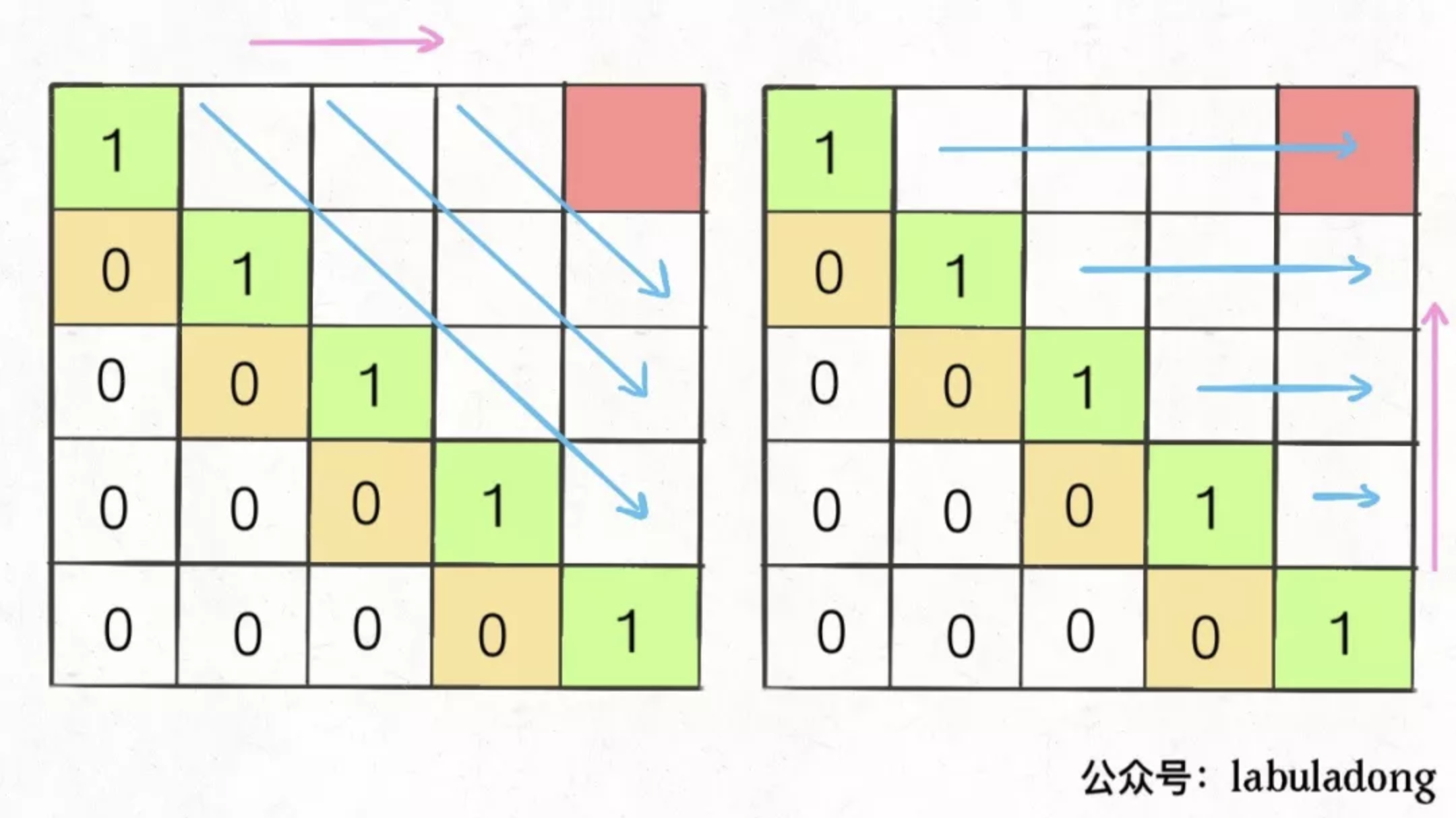
要么从左往右斜着遍历,要么从下向上从左到右遍历,这样才能保证每次 dp[i][j] 的左边、下边、左下边已经计算完毕,最终得到正确结果 。
现在,你应该理解了这两个原则,主要就是看 base case 和最终结果的存储位置,保证遍历过程中使用的数据都是计算完毕的就行了,有时候确实会有多种方法得到正确答案,自行斟酌选择。